
백트래킹(Backtracking)
백트래킹은 문제를 단계적으로 해결하는 알고리즘 기법으로, 가능한 해답을 하나씩 만들어가면서 조건에 맞지 않으면 되돌아가 다른 경로를 시도하는 방식이다. 백트래킹은 가능한 모든 해답을 탐색하면서, 어떤 선택이 조건을 만족하지 않거나 막다른 길에 다다르면 "되돌아가(backtrack)" 다시 다른 선택지를 시도하는 방식을 취한다.
백트래킹, Backtracking 패러다임 조건 및 구조
백트래킹의 조건
백트래킹을 효과적으로 사용하려면 다음의 조건을 만족해야 한다.
- 부분 해의 유효성 검사(Constraint Checking)
- 백트래킹은 매 단계에서 현재까지 만든 부분 해(partial solution)가 유효한지를 확인한다.
- 이 과정에서 문제가 되는 경로는 빨리 포기(Pruning)하여 시간 낭비를 방지한다.
- 목표 상태 검사(Goal Test)
- 백트래킹은 가능한 모든 해를 찾는 것이 목표이므로, 완전한 해(solution)가 구성되었는지, 즉 목표 상태에 도달했는지 검사하는 조건이 필요하다.
백트래킹 구조
백트래킹의 기본 구조는 재귀적 접근을 기반으로 하고, 다음과 같은 단계로 이루어진다.
- 단계별 백트래킹 구조
- 해답 초기 상태 설정
- 백트래킹은 해답을 한 단계씩 구성해 나가는 과정이기 때문에 초기 상태를 설정해줘야한다.
- 재귀적으로 해를 구성
- 매 단계마다 현재 선택할 수 있는 모든 옵션을 탐색한다.
- 이때 각 선택지에 대해 재귀적으로 탐색을 진행하여 해답을 구성해 나간다.
- 유효성 검사(Pruning)
- 각 단계에서 선택한 경로가 유효한지 확인한다.
- 조건을 만족하지 않는 경로라면, 해당 경로를 버리고 다른 선택을 시도한다.
- 이 과정을 가지치기(pruning) 이라 한다.
- 완전한 해 검사
- 만약 부분 해가 완전한 해답이 되었다면, 해당 해답을 기록하거나 반환하여 탐색을 종료한다.
- 만약 해를 찾지 못했다면, backtrack 을 통해 이전 단계로 되돌아가 다른 선택지를 시도한다.
- 백트래킹 수행
- 해답을 찾지 못하고 모든 선택지가 소진시, 현재 단계에서 이전 단계로 돌아가(undo) 다른 경로를 탐색한다.
백트래킹의 동작 원리를 가장 쉽게 파악 할 수 있는 문제를 알아보자.
[백준15649번] N과 M(1)
https://www.acmicpc.net/problem/15649
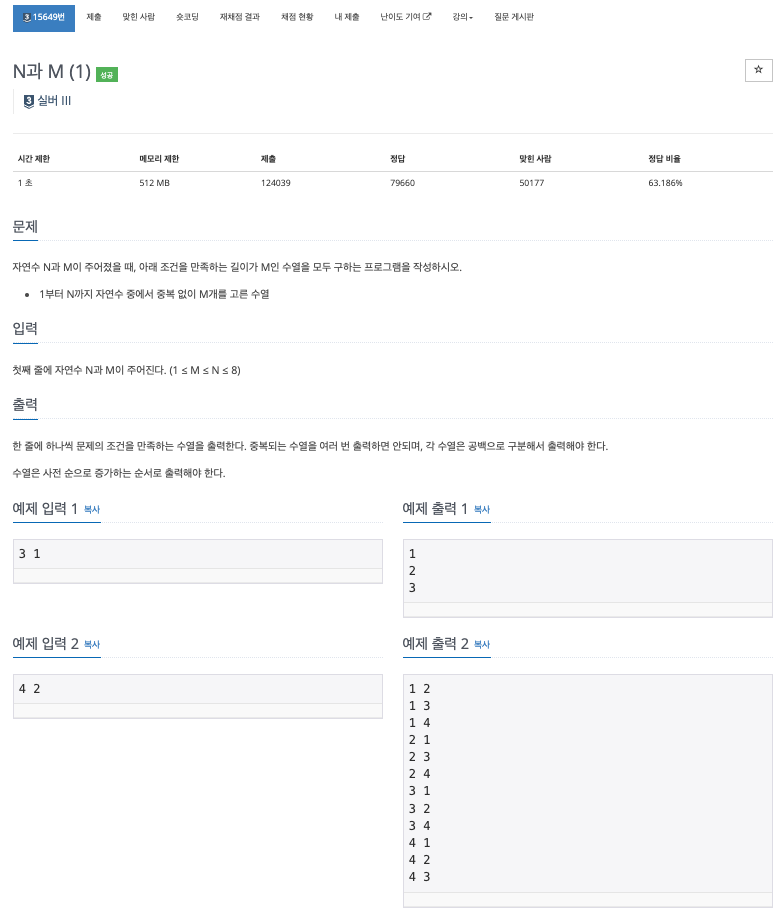
💡구상
이 문제에서 필요로 하는 조건 및 식을 알아보자.
1. 1 부터 N까지 자연수 중에서 중복 없이 M개를 고른 수열
2. N과 M은 1이상 8이하의 자연수
3. 한 줄에 하나씩 문제의 조건을 만족하는 수열을 출력
4. 중복되는 수열을 여러 번 출력하면 안 됨
5. 각 수열은 공백으로 구분하여 출력
6. 수열은 사전 순으로 증가하는 순서로 출력
이 문제는 백트래킹의 동작 원리를 익히는데 아주 좋은 기본적인 문제인것 같다.
백트래킹을 적용해 이문제를 해결하기 위해 다음의 단계로 풀이를 진행했다.
(N은 4, M은 2 의 입력이 들어온 경우를 기준으로 진행)
해답 초기 상태 설정
- N이 4이기 때문에 length가 4인 배열을 만들고 그 배열에 1~4를 할당했다.

재귀적으로 해 구성, 유효성 검사
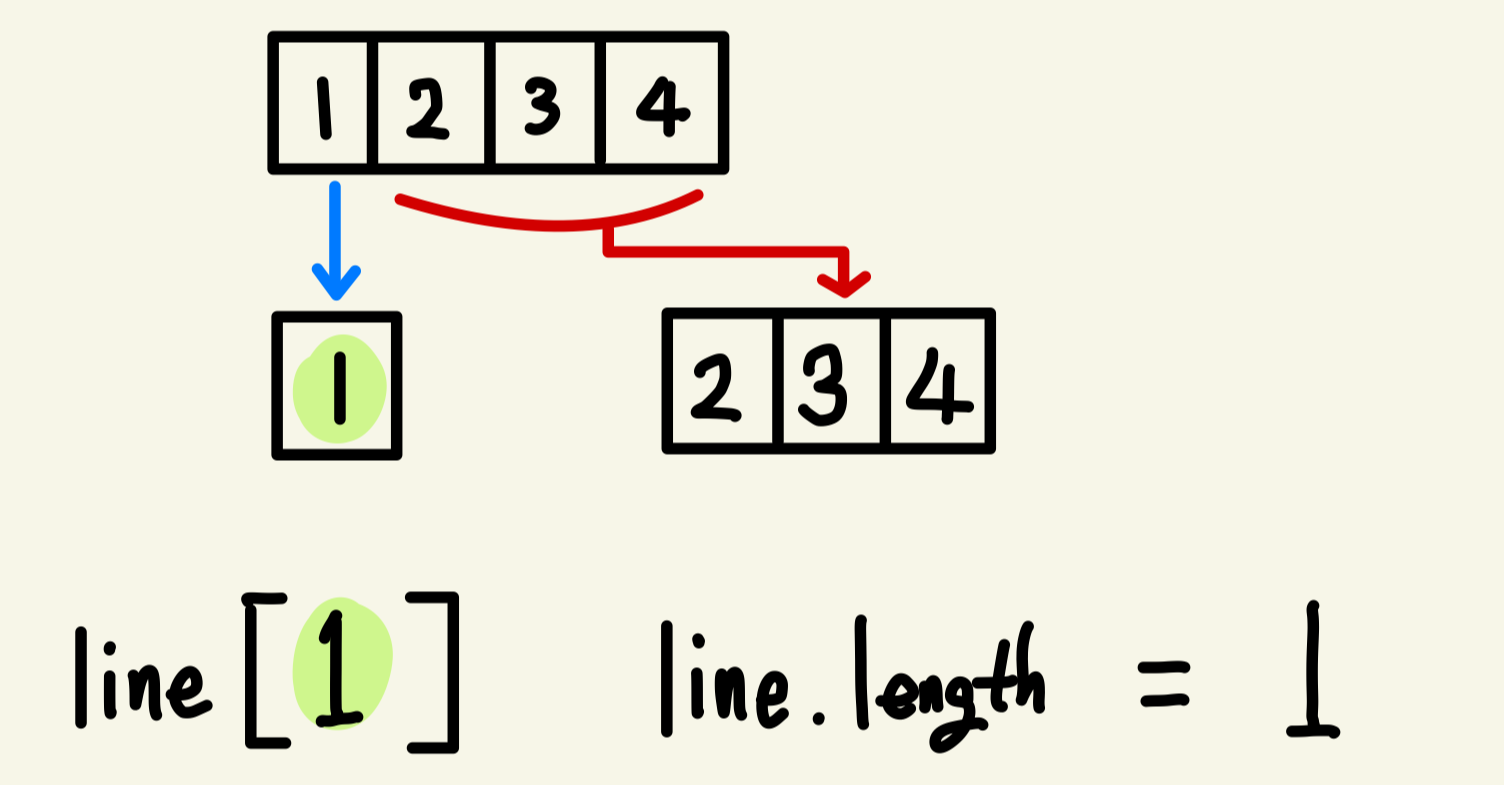
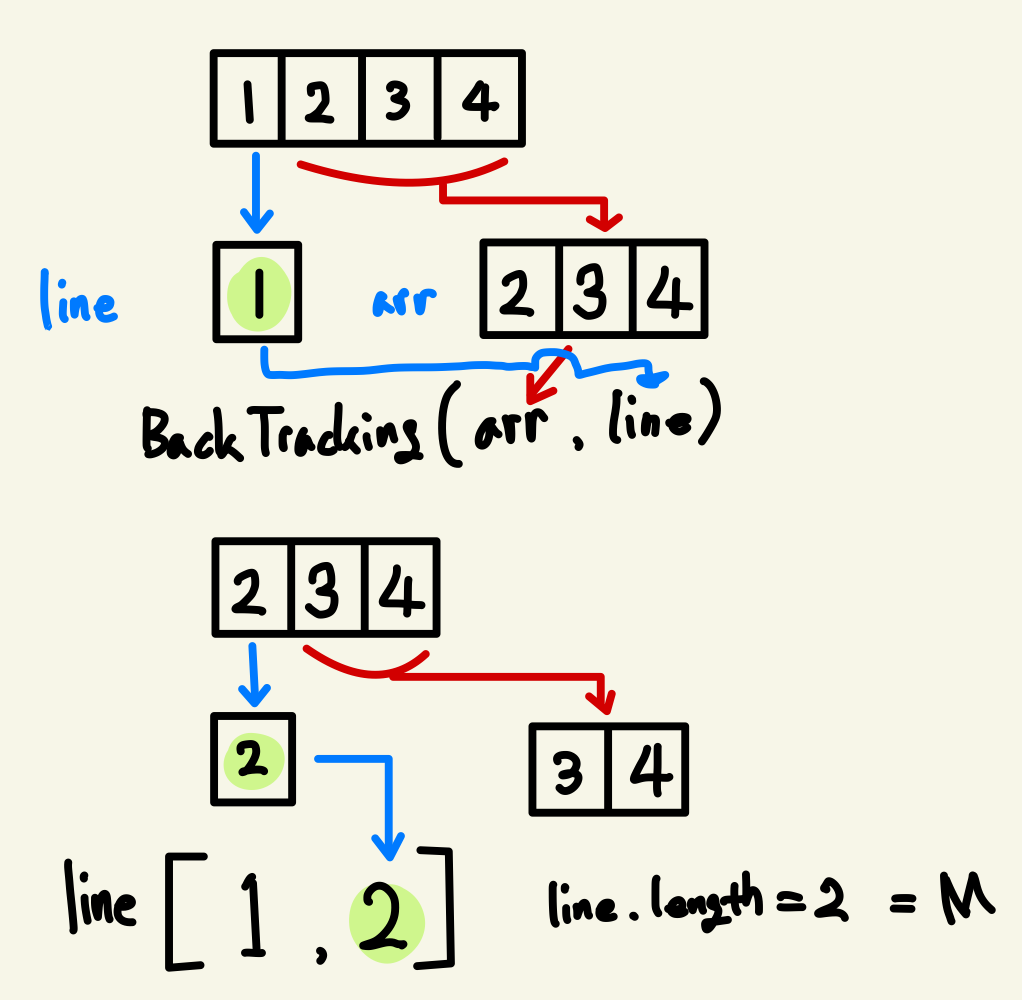
여기서의 핵심은 재귀적으로 해를 구성하며 유효성 검사를 하는 것이다.
위의 그림처럼 처음에 [1, 2, 3, 4]의 배열에서 1 이 line에 들어가게 되었고 line의 길이가 [1] 1 로 M과 일치하지 않음을 판별하여 재귀적으로 함수가 호출되어 이번에는 [2, 3, 4]의 배열과 [1] line 배열을 갖고 반복문을 통해 2를 넣었을 때의 결과와 3, 4 를 각각 넣었을 때의 결과를 바탕으로 line의 길이가 M인지 여부를 통해 완전한 해 여부를 판별한다.
🔍 코드
const [N, M] = require("fs").readFileSync("/dev/stdin", "utf-8").trim().split(" ").map(Number);
const arr = new Array(N).fill(1).map((e, i) => e + i);
const result = [];
const BT = (arr, line) => {
if (line.length === M) return result.push(line.join(" "));
for (let i = 0; i < arr.length; i++) {
const childArr = [...arr];
const childLine = [...line];
childLine.push(...childArr.splice(i, 1));
BT(childArr, childLine);
}
};
for (let i = 0; i < arr.length; i++) {
const childArr = [...arr];
const childLine = [];
childLine.push(...childArr.splice(i, 1));
BT(childArr, childLine);
}
console.log(result.join("\n"));
처음에 작성해서 통과한 코드를 보면 불필요한 반복문으로 코드의 양은 늘고, 가독성은 줄어들었다.
백트래킹 알고리즘을 정리하면서 이 부분을 다시 작성해보기로 하였고 아래와 같이 불필요한 반복문의 중복을 제거하였다.
const [N, M] = require("fs").readFileSync("/dev/stdin", "utf-8").trim().split(" ").map(Number);
const nums = new Array(N).fill(1).map((e, i) => e + i);
const result = [];
const backTracking = (arr, line) => {
if (line.length !== M) {
const len = arr.length;
for (let i = 0; i < len; i++) {
const copyArr = [...arr];
const copyLine = [...line];
const num = copyArr.splice(i, 1);
copyLine.push(num);
backTracking(copyArr, copyLine);
}
} else {
result.push(line.join(" "));
line = [];
}
};
backTracking(nums, []);
console.log(result.join("\n"));
백트래킹은 거의 모든 경우의 수를 순회한다는 면에서 브루트 포스 알고리즘과 비슷하다. 실제로 브루트 포스의 개선 버전으로도 불리는 것 같다. 하지만, 브루트 포스는 조건을 만족하든 안 하든 모든 경우를 전부 순회한다는 점에서 백트래킹과 다르다. 백트래킹은 모든 경우를 순회 하지만, 조건을 만족하지 않으면 그 루트를 버리는 방식으로 동작하기 때문에 시간 단축을 이루어 낼 수 있다.
🔥 배운점
백트래킹을 공부하면서 처음에는 백트래킹의 원리를 이미지화한 자료를 통해 학습을 했는데, 원리에 대해선 이해가 갔으나 그것을 코드로 구현하려니 접근을 어떻게 해야할지 많이 고민되었던거 같다. 다른 해결법을 보면 굳이 배열을 만들지 않고도 해결한 코드를 보았는데, 위의 15649번 문제는 백트래킹의 완전 기본 동작 원리를 위한 문제였기 때문에 괜찮을거 같은데, 만약 조건이 더 붙는다면 배열 없이 해결이 가능할지 궁금해졌다.
백트래킹을 사용하면 가지치기를 통해 조건에 맞지 않는 경로를 빠르게 차단해, 브루트 포스였으면 끝까지 해야하는 불필요한 연산을 줄여 획기적으로 시간 단축을 할 수 있음을 알았다.
백트래킹을 적용하다보니 다른 사람의 풀이에서는 DFS로 문제를 해결한 것을 보았는데 어떻게 다른지, 어떤 방식이 더 효율적인지에 대한 학습을 추가로 진행해야겠다.
'Algorithm' 카테고리의 다른 글
| [알고리즘] 백준 1904 01타일 (1) | 2024.12.26 |
|---|---|
| [알고리즘] 백준 1003 피보나치 함수 (1) | 2024.12.12 |
| [알고리즘] 동적계획법, DP(Dydamic Programming) (0) | 2024.09.19 |
| [알고리즘] 완전 검색, 무차별 대입 검색(Brute Force Search) (0) | 2024.08.17 |
| [알고리즘] 탐욕법, Greedy Algorithm (5) | 2024.08.12 |